一、什么是回归？

孩子的身高是否与父母有关？

实际上，父母和孩子的身高是受到回归效应影响的。在时间纵轴上受影响、具有随机性的事物，无不遵循这一规律。

只要数据足够大，人类的身高或者智商，都有趋于平均值的回归性。

1.1 回归与函数逼近

function approximation or regression

P.S. Reinforcement learning 以及 Regression

均是被误用的名词，但约定俗成沿用至今。so，请理解真正含义。

1.2 多项式的阶数

联想之傅里叶级数：

低阶决定形状，高阶决定细节

回到多项式的阶数，高阶多项式可利用自由度将误差降低。

but，过高的阶数可能导致模型过拟合

如图，高阶拟合可降低误差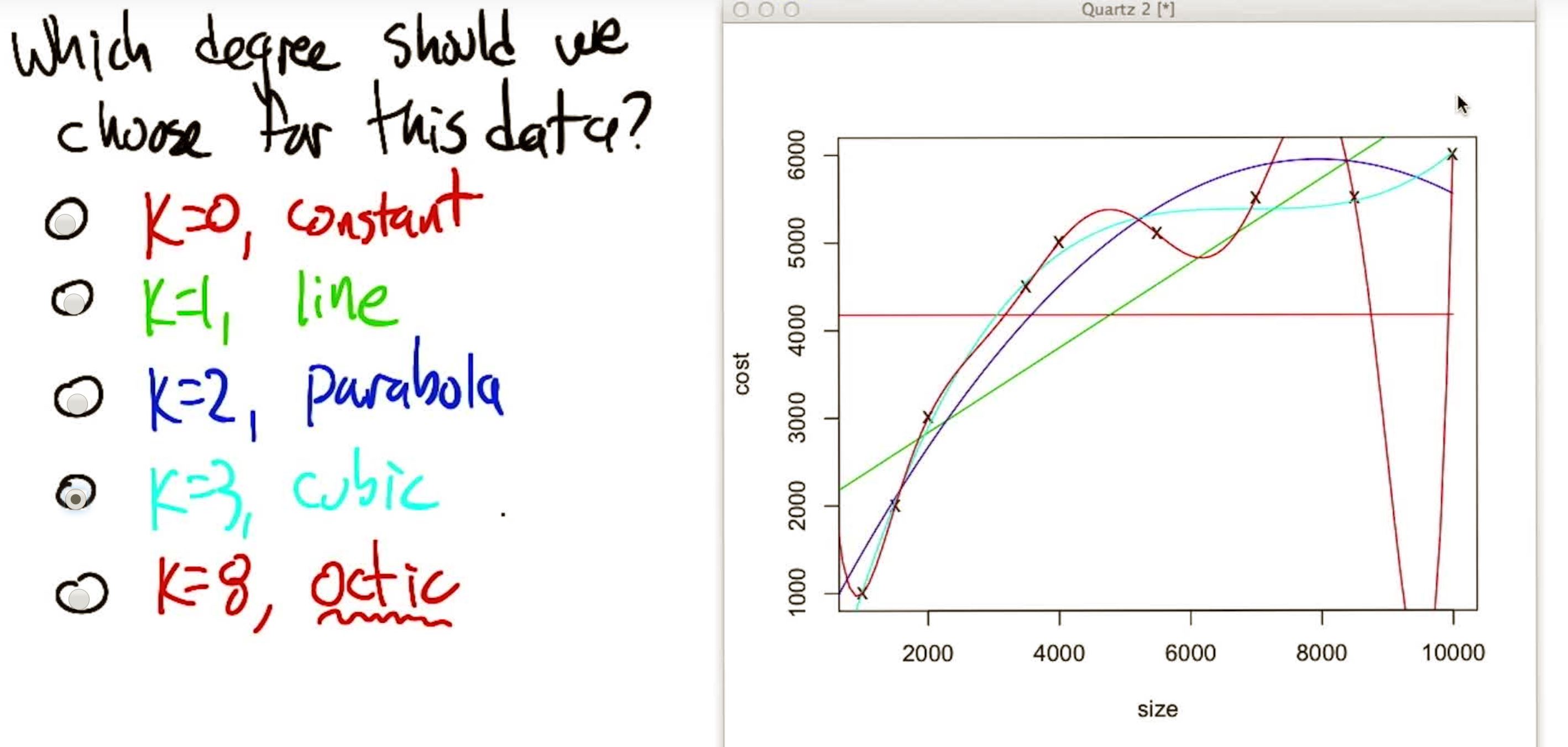

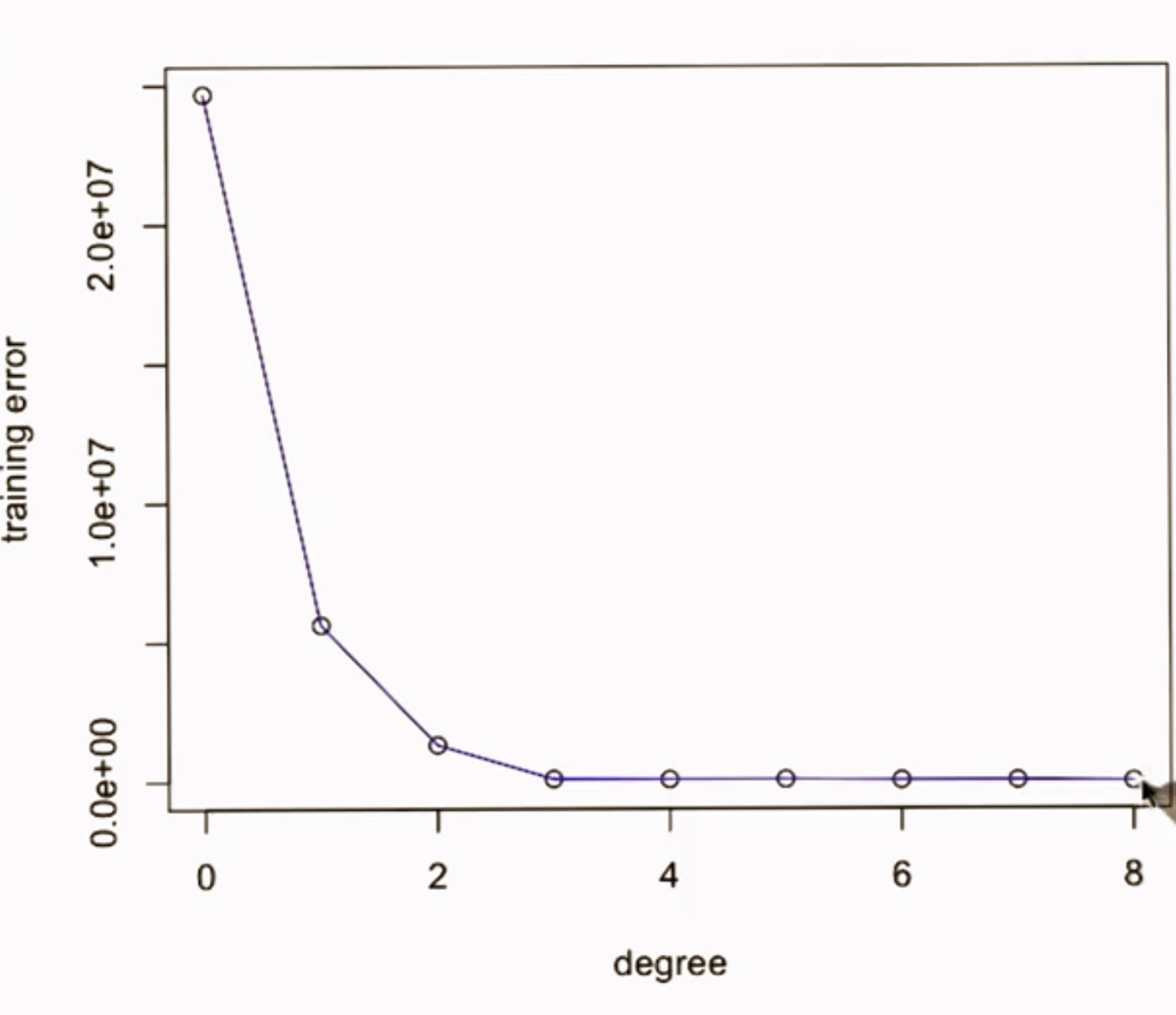
如图 ，误差与拟合多项式阶数的关系

二、多项式回归

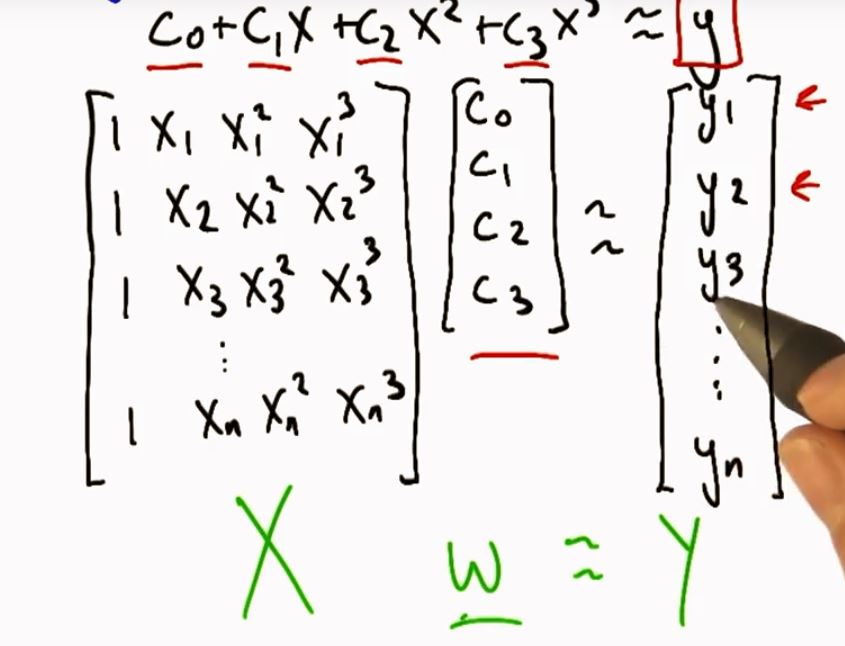
多项式求系数——Review Linear Algebra

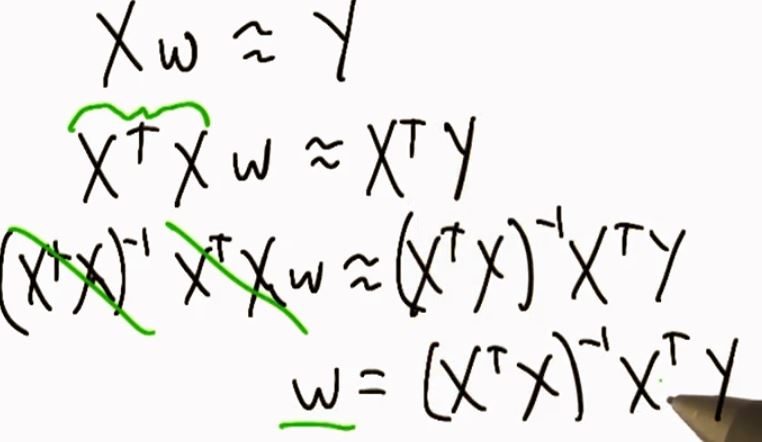
求系数——矩阵运算